Which Two Vectors Add Together To Give A Resultant With The Smallest Magnitude?

Vectors have both magnitude and direction, ane cannot but add two vectors to obtain their sum. The addition of vectors is not as straightforward as the addition of scalars. To better understand this, let us consider an example of a auto travelling x miles North and ten miles South. Hither, the total altitude travelled is 20 miles simply the displacement is nix. The Northward and Southward displacements are each vector quantities, and the opposite directions crusade the private displacements to cancel each other out. In this commodity, let us explore ways to carry out the addition and subtraction of vectors.
Table of Content

What is Vector Addition?
Triangle Police force of Vector Addition
Parallelogram Law of Vector Improver
Polygon Police of Vector
Vector Subtraction
Oftentimes Asked Questions-FAQs

Vector Addition:Triangle, Parallelogram and Polygon Police force of Vectors

Every bit already discussed, vectors cannot be simply added algebraically. Following are a few points to remember while adding vectors:

Vectors are added geometrically and not algebraically.
Vectors whose resultant have to be calculated behave independently of each other.
Vector Addition is nothing but finding the resultant of a number of vectors interim on a torso.
Vector Addition is commutative. This means that the resultant vector is independent of the order of vectors.

Triangle Law of Vector Addition

The vector improver is done based on the Triangle police. Let usa encounter what triangle police of vector addition is:

Suppose there are two vectors:

\(\begin{array}{fifty}\overrightarrow{a}\end{array} \)

and

\(\begin{array}{l}\overrightarrow{b}\terminate{array} \)

Now, depict a line

\(\begin{array}{fifty}AB\end{array} \)

representing

\(\begin{array}{l}\overrightarrow{a}\end{array} \)

with

\(\brainstorm{array}{l}A\end{assortment} \)

as the tail and

\(\begin{assortment}{l}B\terminate{array} \)

as the head. Depict another line

\(\brainstorm{array}{l}BC\end{array} \)

representing (

\(\begin{array}{50}\overrightarrow{b}\end{assortment} \)

) with

\(\brainstorm{assortment}{l}B\cease{array} \)

as the tail and

\(\begin{array}{l}C\end{array} \)

as the head. Now bring together the line

\(\begin{assortment}{l}Ac\end{assortment} \)

with

\(\begin{assortment}{l}A\cease{array} \)

equally the tail and

\(\brainstorm{array}{l}C\stop{array} \)

every bit the head. The line

\(\begin{array}{l}Air-conditioning\end{array} \)

represents the resultant sum of the vectors

\(\begin{array}{50}\overrightarrow{a}\stop{array} \)

and

\(\begin{assortment}{l}\overrightarrow{b}\cease{array} \)

Vector Addition

The line Ac represents

\(\begin{array}{l}\overrightarrow{a}\cease{array} \)

\(\begin{array}{50}\overrightarrow{b}\end{assortment} \)

The magnitude of

\(\begin{array}{l}\overrightarrow{a}\end{array} \)

\(\begin{array}{fifty}\overrightarrow{b}\end{array} \)

is:

\(\begin{array}{l}\sqrt{a^2~+~b^2~+~2ab~cos~\theta}\end{array} \)

Where,

\(\begin{array}{l}a\cease{assortment} \)

= magnitude of vector

\(\begin{array}{50}\overrightarrow{a}\end{assortment} \)

\(\begin{array}{50}b\cease{array} \)

= magnitude of vector

\(\begin{array}{50}\overrightarrow{b}\finish{array} \)

\(\begin{assortment}{l}\theta\end{array} \)

= bending betwixt

\(\begin{array}{l}\overrightarrow{a}\end{array} \)

and

\(\begin{array}{l}\overrightarrow{b}\stop{array} \)

Let the resultant make an angle of

\(\begin{array}{fifty}\phi\stop{array} \)

with

\(\brainstorm{assortment}{fifty}\overrightarrow{a}\stop{array} \)

, then:

\(\begin{array}{fifty}tan\phi\end{array} \)

\(\begin{array}{fifty}\frac{b~sin~\theta}{a~+~b~cos~\theta}\cease{array} \)

Permit us understand this by the means of an case. Suppose there are two vectors having equal magnitude

\(\begin{array}{fifty}A\end{array} \)

, and they make an angle

\(\begin{array}{l}θ\end{array} \)

with each other. Now, to find the magnitude and direction of the resultant, we will use the formulas mentioned above.

Permit the magnitude of the resultant vector be

\(\begin{assortment}{50}B\end{assortment} \)

\(\begin{array}{50}B\terminate{assortment} \)

\(\begin{array}{l}\sqrt{A^two~+~A^ii~+~2AA~cos~\theta}\end{array} \)

\(\brainstorm{array}{l}two~A~cos~\frac{θ}{2}\end{array} \)

Let'southward say that the resultant vector makes an angle

\(\brainstorm{array}{l}Ɵ\stop{array} \)

with the first vector

\(\begin{array}{50}tan~\phi\end{array} \)

\(\brainstorm{assortment}{l}\frac{A~sin~θ}{A~+~A~cos~θ}\cease{array} \)

\(\begin{array}{l}tan~\frac{θ}{ii}\stop{assortment} \)

Or,

\(\begin{assortment}{l}Ɵ\end{assortment} \)

\(\begin{array}{l}\frac{θ}{ii}\terminate{assortment} \)

Parallelogram Law of Vector Addition

The vector add-on may also exist understood past the law of parallelogram. The police states that "If two vectors acting simultaneously at a indicate are represented in magnitude and management by the 2 sides of a parallelogram fatigued from a point, their resultant is given in magnitude and management by the diagonal of the parallelogram passing through that point."

According to this police force, if two vectors

\(\begin{array}{l}\underset{P}{\rightarrow}\end{array} \)

and

\(\begin{array}{l}\underset{Q}{\rightarrow}\end{array} \)

are represented by two next sides of a parallelogram both pointing outwards equally shown in the figure beneath, and then the diagonal drawn through the intersection of the ii vectors represent the resultant.

Parallelogram Law of Vector Addition

In Parallelogram Police of Vector Improver, the magnitude of the resultant is given by:
Magnitude of Resultant Vector
The management of the resultant vector is determined equally follows:
Direction of Resultant Vector

Polygon Police of Vector

According to the polygon law of vector add-on, if the number of vectors can be represented in magnitude and management by the sides of a polygon taken in the aforementioned guild, then their resultant is represented by magnitude and direction such that the endmost side of the polygon is taken in the opposite direction.
Permit

\(\brainstorm{array}{l}\vec{A}\stop{assortment} \)

\(\begin{assortment}{l}\vec{B}\end{array} \)

\(\begin{array}{fifty}\vec{C}\end{array} \)

, and

\(\begin{array}{l}\vec{D}\end{array} \)

exist the iv vectors for which the resultant has to be obtained.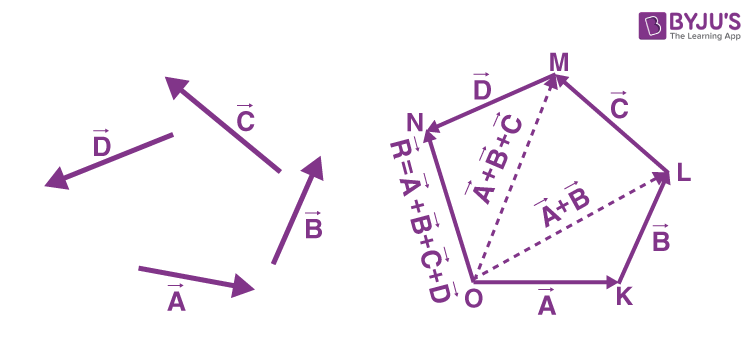
Polygon law of vector addition

Consider triangle OKL, in which the vectors

\(\begin{array}{50}\vec{A}\terminate{array} \)

and

\(\begin{assortment}{l}\vec{B}\end{array} \)

are represented past sides

\(\begin{array}{fifty}\vec{OK}\end{array} \)

\(\begin{assortment}{l}\vec{KL}\end{assortment} \)

and are taken in the same order. Therefore, from triangle constabulary of vector addition we know that the closing side

\(\brainstorm{assortment}{l}\vec{OL}\cease{array} \)

is considered in the opposite management such that it represents the resultant vector

\(\begin{array}{l}\vec{OR}\terminate{array} \)

and

\(\begin{array}{fifty}\vec{KL}\cease{array} \)

.
Therefore,

\(\begin{array}{l}\vec{OK}\end{assortment} \)

\(\begin{array}{l}\vec{KL}\end{array} \)

\(\begin{array}{50}\vec{OL}\terminate{array} \)

eq.ane
From the triangle law of vector improver, we know that triangle OLM can exist expressed as

\(\begin{array}{50}\vec{OM}\cease{assortment} \)

is the resultant of the vectors

\(\begin{array}{fifty}\vec{OL}\end{array} \)

and

\(\brainstorm{assortment}{l}\vec{LM}\end{array} \)

That is,

\(\begin{assortment}{l}\vec{OL}\stop{array} \)

\(\begin{array}{l}\vec{LM}\end{array} \)

\(\begin{array}{l}\vec{OM}\end{array} \)

From eq.ane,

\(\begin{array}{l}\vec{OK}\terminate{assortment} \)

\(\begin{array}{fifty}\vec{KL}\end{array} \)

\(\brainstorm{array}{l}\vec{LM}\end{array} \)

\(\begin{array}{l}\vec{OM}\end{array} \)

eq.2
Again, applying the triangle constabulary of vector addition to triangle OMN,

\(\brainstorm{array}{fifty}\vec{OM}\cease{assortment} \)

\(\begin{array}{50}\vec{MN}\end{array} \)

\(\begin{array}{50}\vec{ON}\cease{array} \)

From eq.ii, we go,

\(\begin{assortment}{l}\vec{OK}\finish{array} \)

\(\begin{assortment}{l}\vec{KL}\end{array} \)

\(\begin{array}{l}\vec{LM}\terminate{array} \)

\(\begin{assortment}{50}\vec{MN}\end{array} \)

\(\begin{array}{l}\vec{ON}\end{assortment} \)

eq.3
Therefore,

\(\begin{array}{l}\vec{OK}\cease{assortment} \)

\(\begin{array}{fifty}\vec{A}\stop{array} \)

\(\begin{array}{50}\vec{KL}\end{array} \)

\(\brainstorm{array}{50}\vec{B}\end{array} \)

\(\begin{array}{l}\vec{LM}\end{array} \)

\(\begin{array}{fifty}\vec{C}\end{array} \)

\(\begin{array}{l}\vec{MN}\end{array} \)

\(\begin{array}{l}\vec{D}\cease{assortment} \)

Because

\(\begin{array}{l}\vec{ON}\end{array} \)

\(\brainstorm{array}{l}\vec{R}\end{array} \)

, the equation becomes

\(\brainstorm{array}{l}\vec{A}\end{array} \)

\(\begin{array}{l}\vec{B}\end{array} \)

\(\begin{array}{l}\vec{C}\stop{assortment} \)

\(\begin{array}{l}\vec{D}\cease{array} \)

\(\brainstorm{assortment}{l}\vec{R}\end{assortment} \)

Click the below video to understand the application of polygon law of vector adding:

Polygon law of vector addition

Vector Subtraction

Subtraction of ii vectors is similar to addition. Suppose

\(\begin{array}{l}\overrightarrow{a}\end{array} \)

is to be subtracted from

\(\brainstorm{array}{50}\overrightarrow{b}\end{array} \)

\(\brainstorm{array}{50}\overrightarrow{a}\stop{assortment} \)

–

\(\begin{array}{50}\overrightarrow{b}\end{array} \)

can be said as the addition of the vectors

\(\begin{array}{l}\overrightarrow{a}\end{assortment} \)

and (-

\(\brainstorm{array}{l}\overrightarrow{b}\end{array} \)

). Thus, the formula for add-on can exist applied as:

\(\begin{array}{fifty}\overrightarrow{a}\end{array} \)

–

\(\brainstorm{array}{50}\overrightarrow{b}\end{assortment} \)

\(\begin{array}{l}\sqrt{a^2~+~b^two~-~2ab~cos~\theta}\end{assortment} \)

\(\begin{array}{l}\overrightarrow{b}\end{array} \)

) is zippo simply

\(\brainstorm{array}{fifty}\overrightarrow{b}\end{assortment} \)

reversed in management.

Related manufactures:

Oft Asked Questions – FAQs

What is the maximum and minimum sum of 2 vectors?

The maximum sum of ii vectors are obtained when the two vectors are directed in the same direction. The minimum sum is obtained when the two vectors are directed in the opposite direction.

Is vector add-on commutative?

Yeah, vector addition is commutative.

Is vector addition applicable to any 2 vectors?

No, vector add-on is not applicable to any two vectors. Two vectors are added only when they are of the same types and nature. For case, ii velocity vectors can be added simply one velocity vector and one strength vector cannot be added.

Country the associative property of vector addition.

The associative property of vector add-on states that the sum of the vectors remains the aforementioned regardless of the club in which they are arranged.

Tin can the sum of two vectors have a null?

Yeah, two vectors with equal magnitude and pointing in opposite directions will have sum equal to cypher.

Stay tuned with BYJU'S to learn more than almost vectors, vector note and much more than.